СТАТИКА ТВЕРДОГО ТЕЛА

 ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И АКСИОМЫ СТАТИКИ

    Статикой (от греческого слова «стасис»—неподвижное состояние, покой) - называется учение о равновесии сил, действующих на твердое тело, а также о замене одних систем другими, им эквивалентными.
Статика есть частный случай динамики, поскольку динамика изучает движение под действием сил, а равновесие — частный случай движения. В ней рассматриваются две основные задачи: 1) сложение сил и приведение системы сил, действующих на абсолютно твердое тело, к простейшему виду; 2) определение необходимых и  достаточных условий равновесия действующих на абсолютно твердое тело систем сил.
    Изучение теоретической механики обычно начинают со статики твердого тела, так как ее методы широко применяются во многих технических дисциплинах.
    Как уже отмечалось, для механики важен эффект, который производят действующие на тело силы, т. е. изменение механического состояния тела. Если изменение механического состояния тела выражается в изменении скорости его движения (в частности, в изменении равновесия тела), то тогда говорят о динамическом проявлении силы.
Если же в результате действия одного тела на другое характер движения не изменяется, в частности, не нарушается состояние равновесия другого тела, то в таком случае говорят о статическом проявлении силы.
Как известно из опыта, действие силы на тело определяется следующими тремя элементами: 1) численным значением (модулем) силы, 2) направлением силы и 3) точкой приложения силы. Понятие силы в механике имеет научную ценность потому, что ее можно измерять. Измерение силы в механике основано на сравнении с однородной величиной, условно принятой за единицу измерения (эталон). При этом две сравниваемые силы считают равными, если их действия на тело в одних и тех же условиях одинаковы.
   Приборы, служащие для статического сравнения и измерения сил, называются динамометрами (силомерами). Примером простейшего динамометра служат обыкновенные пружинные весы.
    В технической системе единиц (МКГСС) за единицу силы принимают килограмм силы (сокращенно — кГ), т. е. вес международного эталона, приблизительно равный весу одного кубического дециметра чистой воды при 4° С на уровне моря и на широте 45°. В Международной системе единиц (СИ) за единицу силы принимается сила, называемая ньютоном (сокращенно—н).

Заметим, что 1 кГ = 9,81 н или 1н=0,102 кГ  т. е. ньютон примерно в 10 раз меньше силы в 1 кГ.
Выбор  международной единицы силы основан на динамическом определении силы.

    Направлением силы есть  направление того прямолинейного движения, которое данная сила сообщила бы точке ее приложения, если бы эта частица тела была свободна и находилась до этого в покое.
Прямая, по которой направлена сила, называется линией действия силы.
Точкой приложения силы называется та материальная частица тела, к которой сила непосредственно приложена.
Таким образом, сила является векторной величиной. Заметим, что силу нельзя рассматривать как свободный вектор, так как точку приложения силы нельзя выбирать произвольно.
Сила, как и всякий вектор, изображается направленным отрезком (со стрелкой на конце). Длина этого отрезка (АВ на рис. 16) выражает в выбранном масштабе модуль силы, его начало (точка А) обычно совпадает с точкой приложения силы.

   Прямая DЕ называется линией действия силы.
Силу, как и всякую векторную величину, будем обозначать одной буквой со стрелкой над ней (например ) или двумя буквами со стрелкой над ними (например ). Модуль силы обозначается той же буквой, но без стрелки над ней, например F, или заключением вектора в прямые скобки //.
   Теперь выясним понятие системы сил, механической эквивалентности системы сил, а также понятие взаимно-уравновешивающихся сил.
1. Совокупность сил, одновременно действующих на данное тело, называется системой сил.
  Силы, входящие в состав данной системы, называются составляющими. .
2. Если одну систему Сил, действующих на данное свободное тело, можно заменить другой, не изменяя при этом равновесия или движения, в котором находится тело, то такие две системы сил будут эквивалентными.
З. Свободным телом называется тело, не скрепленное с другими телами, т. е. тело, которому можно сообщить любое перемещение в пространстве.
Система сил, под действием которой свободное твердое тело может находиться в равновесии, называется уравновешенной, или эквивалентной нулю.
4. Если данная система сил эквивалентна одной силе, то такая сила называется равнодействующей данной системы сил. Таким образом, равнодействующая — это сила, которая эквивалентна данной системе сил, т. е. одна заменяет действие данной системы сил на твердое тело.
  Нахождение равнодействующей называется сложением сил, а замена одной силы системой сил, действующих на тело так же, как и данная сила, называется разложением сил. В дальнейшем мы увидим, что не всякая система сил может быть заменена одной силой, и, следовательно, не всякая система сил имеет равнодействующую.
 5. Если под действием данной системы сил свободное тело не
изменяет своего движения или, в частности, продолжает оставаться
в равновесии, то она называется уравновешенной системой, или
системой, эквивалентной нулю. Говорят также, что эта система сил находится в равновесии.
6. Сила, которая, будучи присоединена к некоторой системе сил, действующих на тело, приводит ее в равновесие, называется уравновешивающей силой данной системы. Уравновешивающая сила равна по величине равнодействующей силе, но направлена в сторону, ей противоположную.
 Чтобы твердое тело находилось в равновесии под действием некоторой системы сил, последние должны удовлетворять опреде-ленным условиям равновесия. Нахождение этих условий является одной из основных задач статики. Но для того, чтобы определить условия равновесия различных систем сил, а также решить ряд других задач механики, необходимо уметь складывать силы, дей-ствующие на твердое тело, заменять одну систему сил другой и при-водить данную систему сил к простейшему виду.
Силы, действующие на твердое тело, делятся на активные, или задаваемые, и реакции связей. Связи играют большую роль в датике и будут рассмотрены подробно позже.
   Активными силами в технике являются различные нагрузки. Они могут быть сосредоточенными и распределенными.
Сосредоточенной называется сила, приложенная к телу в какой-нибудь одной точке. Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.
Понятие о сосредоточенной силе является условным, так как практически приложить силу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, представляют собой по существу равнодействующие некоторых систем распределенных сил, например, сил тяжести тел. Сосредоточенные нагрузки будем обозначать буквами 

 

     В технических расчетах часто приходится встречаться с нагрузками, распределенными вдоль данной поверхности по тому или иному закону.
    Распределенная система сил характеризуется интенсивностью q, т. е. величиной силы, приходящейся на единицу длины нагруженного отрезка. Измеряется интенсивность в ньютонах или килограммах, деленных на метры (н/м или кГ/м).
Рассмотрим некоторые простейшие примеры распределенных сил, лежащих в одной плоскости.
1. Силы, равномерно распределенные вдоль отрезка прямой (рис. 17, а). Для такой системы сил интенсивность q — величина постоянная. При статических расчетах эту систему сил можно заменить равнодействующей  По модулю

где а — длина отрезка, вдоль которого распределена нагрузка.
2. Силы, распределенные вдоль отрезка прямой по линейному закону (рис. 17, б). Примером такой нагрузки могут служить силы давления воды на плотину, величина которых наибольшая у дна и падает до нуля у поверхности воды. Для этих сил интенсивность q — величина переменная, растущая от нуля до максимального значения qmax.

Равнодействующая таких сил определяется аналогично равнодействующей сил тяжести, действующих на однородную треугольную пластину. Поскольку вес однородной пластины пропорционален ее площади, то по модулю

                                                                   

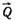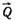Линия действия силы  проходит на расстоянии а/3 от qmax.

3. Силы, равномерно распределенные по дуге окружности (рис. 17, в), например, силы q гидростатического давления на боковые стенки цилиндрического сосуда. Из симметрии, ясно, что сумма проекций этих сил на ось Оу, перпендикулярную оси симметрии Ох,
равна нулю. Следовательно, их равнодействующая Q направлена вдоль оси Ох.
  По модулю   

                                                                        

где h— длина хорды, стягиваемой дугой 

Силы, действующие на твердое тело, можно разделить также на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.
   Внутренние силы возникают в телах под действием внешних.

  Основной задачей статики является исследование условий равновесия внешних сил, приложенных к абсолютно твердому телу. Для выявления внутренних усилий, возникающих в конструкциях под действием внешних сил, используют метод сечений, который Эволяет свести определение внутренних сил в твердом теле к определению сил внешних. Этот метод заключается в следующем: мысленно разрезают тело плоскостью там, где хотят определить внутренние силы, отбрасывают любую отрезанную часть тела и заменяют действие отброшенной части силой, которая будет внешней для рассматриваемой части тела. Из условий равновесия определяют указанную силу. Метод сечений особенно широко используют в курсе «Сопротивление материалов».